Why Past ENSO Cases Aren’t the Key to Predicting the Current Case
Lately, many of us are wondering if a 2014-15 El Niño is going to materialize, and if so, how strong it might become and how long it will last. It might cross some folks’ minds that the answer to these questions can be found by collecting past ENSO cases that are similar and see what happened. Such an approach is known as analog forecasting, and on some level it makes intuitive sense.
In this post, I’ll discuss why the analog approach to forecasting often delivers disappointing results. Basically, it doesn’t work well because there are usually very few, if any, past cases on record that mimic the current situation sufficiently closely. The scarcity of analogs is important because dissimilarities between the past and the present, even if seemingly minor, amplify quickly so that the two cases end up going their separate ways.
Past Cases (Analogs) Similar to 2014
The current situation is interesting because it seems we have been teetering on the brink of El Niño, as our best dynamical and statistical models keep delaying the onset but yet continue to predict the event starting in fairly short order. Which raises the question: have there been other years that have behaved similarly to 2014? Before we check, let’s talk for a minute about how we find good analogs for the current situation.
The set of criteria by which the closest analogs are selected is a contested issue in forecasting. One can select years based on time series, maps, or among many variables across different periods of time. There are also many different ways to measure similarity, and one has to select the appropriate level of closeness to past cases—in other words, decide how close is close enough.
One main criticism of analog forecasting is the subjectivity of making such choices, which can lead to different answers. Here, I will use one method based on similarities of sea surface temperature (SST) in the Nino3.4 region (1). Figure 1 shows six other years during the 1950-2013 period that have behaved similarly to this year in terms of SST, and also shows what happened in the seven months following September.
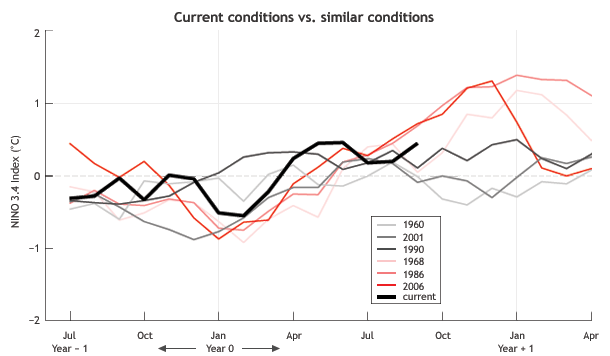
Figure 1. Monthly average SST anomaly in the Nino3.4 region over the last 15 months for this year (thick black line), and the same for 6 other years selected as the closest analogs for this year. After September, the last month for which we have observations for this year, the ENSO behavior of the chosen analog cases is shown for the following seven months, providing a basis for a possible analog forecast for the current year. Photo credit: IRI, Columbia University and NOAA Climate Program Office.
In checking out the analog forecast possibilities in Fig. 1, it is clear that the outcomes are diverse. Out of the six selected cases, three indicate ENSO-neutral for the coming northern winter season, while the other three show El Niño (at least 0.5˚ anomaly)—and all three attain moderate strength (at least 1˚C anomaly) for at least one 3-month period during the late fall or winter (2). For the coming January, the 6 analogs range from -0.3 to 1.4˚C, revealing considerable uncertainty in the forecast (3).
Although this uncertainty in outcomes is somewhat smaller than that what we would have if we selected years completely randomly from the history, it is larger than that from our most advanced dynamical and statistical models. This is one reason analog forecasting systems have been largely abandoned over the last two decades as more modern prediction systems have proven to provide better accuracy.
Why Analogs Often Don’t Work Well
The large spread among the six analog cases selected for a current ENSO forecast is not unusual, and it would be nearly as large even if we came up with a more sophisticated analog ENSO forecast system (4). The big problem in analog forecasting is the lack of close enough analogs in the pool of candidates.
Furthermore, the criteria by which we select cases always ignore some relevant information, and this missed information introduces differences between the current case and the past analog cases. Even if we knew and included everything that did matter, the fact that the ocean and atmosphere are fluids means that tiny differences between the current and past cases often quickly grow into larger differences.
Van den Dool (1994)’s ”Searching for analogs, how long must we wait?” calculates that we would have to wait about 1030 years to find 2 observed atmospheric flow patterns that match to within observational error over the Northern Hemisphere. While the ocean is not as changeable as the atmospheric flow, it is clear that finding close matching analogs would also require a very long historical dataset.
Even finding good matches with the relatively simple Nino3.4 time series is an obstacle (see the left side of Fig. 1). In the case of ENSO, there are only ~60 years in the “well observed” historical record of tropical Pacific sea surface temperatures and even fewer cases of El Niño or La Niña years. The severe shortness of the past record prevents an analog approach from bearing much fruit. More complex statistical and coupled ocean-atmosphere dynamical models can make better predictions than analogs.

Figure 2. Monthly average SST anomaly in the Nino3.4 region over the last 15 months for this year (thick black line), and the same for 6 other years selected as the closest analogs for this year. This figure goes 9 months farther out into the future than Fig. 1, and most of the future portion of Fig. 1 is contained in the box labeled “upcoming winter”. Note that the medium-bright red line, for 1986-87, shows the rare event of two consecutive years of El Niño, and that the very light red line, for 1968-69, shows a weaker case of the same. Photo credit: IRI, Columbia University and NOAA Climate Program Office.
Yet, despite the above warning, forecasters continue to enjoy identifying analogs when we consider what ENSO might have up its sleeve for the forthcoming seasons. For example, notice in Fig. 2, which shows what happened with each of the 6 analogs nine months farther into the future than shown in Fig. 1, that in early autumn 1986 (medium red line), a late-starting El Niño attained moderate strength during 1986-87, but also continued for a second year and reached even greater strength in 1987-88.
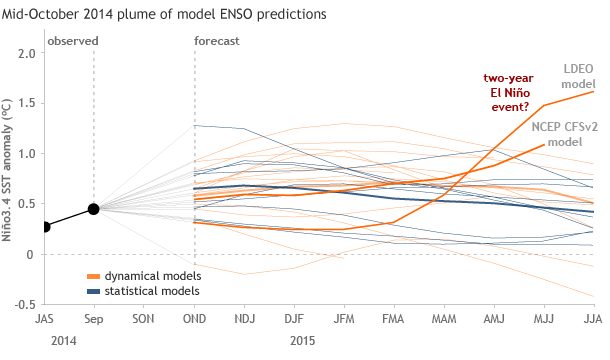
Do late-starting El Niño events tend to endure into a second ENSO cycle and take two years instead of one to run their course? While that is a topic for another post, let’s just say that there have been so few cases of two-year events that it would be foolhardy to actually predict one without more evidence. Interestingly, though, two of the models on this month’s IRI/CPC ENSO forecast plume (Fig. 3) do suggest the possibility of an El Niño both this year and a second year (2015-16). One of those models is NOAA/NCEP’s own CFSv2, and another is the Lamont-Doherty Earth Observatory (LDEO) intermediate model. Could they be on to something?
Figure 3. ENSO prediction plume from September 2014 (see official version of this graphic), for SST anomaly out to Jun-Jul-Aug 2015. The orange lines show predictions of individual dynamical models, and blue lines those of statistical models; the thicker lines show the averages of the predictions from those two model types. The black lines and dots on the left side show recent observations. A weak El Niño (SST of at least 0.5˚, but less than 1˚C anomaly) continues to be predicted for late fall and winter 2014-15 by many of the dynamical and statistical models. The NCEP CFSv2 and the LDEO dynamical models, highlighted in brighter orange, suggest continuation and intensification of El Niño in spring 2015, presaging a possible 2-year event, as occurred in 1986-87-88 (but the LDEO model holds back on a full-fledged El Niño for the first year).
Footnotes
(1) This method uses the 13 months prior to (and including) the most recently completed month, but weights the more recent months more heavily than the less recent ones. In the case of Fig. 1, the relative weights from September 2013 through September 2014 are .02, .02, .03, .05, .06, .06, .07, .09, .10, .11, .12, .14, and .13. This weighting pattern was based on correlations between the earlier and current SSTs, averaged over all starting/ending times of the year. In a more refined system, the weighting pattern would change noticeably depending on these starting/ending times of the year. This variation exists due to the typical seasonal timing of ENSO events. For example, the correlation between SST in February with that in July is low, while the correlation between SST in September with that in February is quite a bit higher, as many ENSO events begin during summer and last through the following winter.
So, as we might expect from the weighting pattern, the similarity between this year and the selected analog years is seen in Fig. 1 to be greatest over the most recent 3 to 5 months. The closeness of the match is calculated as the square root of the sum of the weighted squared differences between the Nino3.4 SST this year and the candidate year. This metric is often called the Euclidean distance, and the smaller the number, the better the analog match.
(2) The time unit used in this analog prediction system is 1-month, in contrast to the 3-month averages usually used by NOAA in ENSO diagnostics and prediction.
(3) This spread is occurring at a time of year when persistence (i.e., maintenance over time of either positive or negative anomalies of SST) is typically strong and so forecasts using just recent observations generally do better than at other times of the year.
(4) More sophisticated analog systems used in earlier decades for seasonal climate forecasting are documented in Barnett and Preisendorfer 1978, Livezey and Barnston 1988, and Barnston and Livezey 1989.
References
Barnett, T. P., R. W. Preisendorfer, 1978: Multifield analog prediction of short-term climate fluctuations using a climate state vector, J. Atmos. Sci., 35, 1771–1787.
Barnston, A. G., and R. E. Livezey, 1989: An Operational Multifield Analog/Anti-Analog Prediction System for United States Seasonal Temperatures. Part II: Spring, Summer, Fall and Intermediate 3-Month Period Experiments. J. Climate, 2, 513–541.
Livezey, R. E., and A. G. Barnston, 1988: An operational multifield analog/antianalog prediction system for United States seasonal temperatures: 1. System design and winter experiments. J. Geophys. Res., Atmospheres, 93, D9, 10953–10974. DOI: 10.1029/JD093iD09p10953
Van den Dool, H. M., 1994: Searching for analogues, how long must we wait? Tellus A, 46, 314-324.
Comments
Odd critique of statistical tools
RE: Odd critique of statistical tools
Very good comments. Let's take them one at a time, and in order.
To be sure, dynamical modelers must also make subjective decisions, such as about which processes are to be included in the model. Presumably, scale analyses can help determine the relative priorities. Also, not everything can be included explicitly, and some important processes (like tropical convection) must be abbreviated using statistical parameterization schemes. In that sense, the choice of which physics to include, and how to include it, in dynamical models parallels the choice of the criteria for matching in analog forecasting. However, the way in which analogs are composited into a single forecast is likely to be more crude than the way in which a full ensemble of model runs is used for a climate forecast. In the example shown here, only 6 past cases were selected, and each of them had obvious deviations from the current case over the selection period. Most climate model ensemble runs manage to include a lot more than 6 ensemble members. Perhaps a more important difference between the two methods is the level of explicitness in representing the physics in dynamical models, compared with the black box style of making an analog forecast. Although this in itself does not necessarily mean the long-term forecast skill will be higher in dynamical models, it does mean that part of the forecast job is nailed down in a more precise manner by representing the underlying physics exactly. Yet the bottom line skill averages are what really determine the relative worth of the two approaches. So let's look at that. Since analog methods have generally not continued as a current method to develop climate forecasts, it is hard to compare their skill with that of today's leading dynamical models. It is assumed that the dynamical models deliever higher skill, on average, than analog systems. Perhaps this needs to be demonstrated in a formal way, and of course it is possible that the analog approach would still match the dynamical approach, or that the skill difference would not be statistically significant. But I tend to doubt it. In a recent study comparing the real-time forecasts of ENSO forecast models of different types since 2002, the dynamical models tended to have highest skills. (See "Skill of real-time seasonal ENSO model predictions during 2002-11: Is our capability increasing?" by A. G. Barnston, M. K. Tippett, M. L. L'Heureux, Michelle L.; etc. in Bulletin of the AMS, 93, 631-651.)
My comparison between the analog method and more sophisticated statistical method was in the context of the simple analog method used here, where only SST observations over the previous year were used, and where only about 60 years of record are available so that only 6 cases passed as being at least minimally similar toe current case. The lack of enough close matches (or even a single VERY close match) is emphasized. Basing a forecast on a limited set of analogs does allow for some nonlinearity to enter into the forecast, but the luck of the draw on the selected similar cases leads to questionable stability in the forecast implications. In the case of Huug van den Dool's constructed analog, ALL years in the available record are used and given weights (positive or negative), so that the method becomes somewhat like a linear regression method, showing a bridge between analogs and multiple linear regression. Unless the nonlinear component in seasonal climate predictability is substantial, which it has not been shown to be, I favor regression (using all past years of data) to using a limited set of analogs to try to capture nonlinearity in addition to the linear components of the variability. I believe that in using a small set of analogs, sampling variabiity usually outweighs the beneficial incorporation of nonlinearity. This is why I think that more traditional statistical methods are likely to have higher skills than a limited set of analogs, none of which match the current case extremely well.
About the set of analog-derived forecasts shown here for 2014-2015, just because it currently looks similar to the spread of the NCEP CFSv2 model doesn't mean it is as good a method. To compare the skills of the two systems, a hindcast test covering all years (hopefully over 30) would need to be conducted. A single case rarely tells us very much about what level of skill to expect over a long term.
RE: RE: Odd critique of statistical tools
Past ENSO cases, Poor Predictors? Help is in the Air.
RE: Past ENSO cases, Poor Predictors? Help is in the Air.
The main message here is well taken -- namely, that ENSO is not the only game in town when it comes to winter climate prediction in the U.S. Other well-known climate patterns such as AO, NAO, EP/NP, and others can play important roles also. In fact, we had two blog pieces about some of these other patterns: http://www.climate.gov/news-features/blogs/enso/other-climate-patterns-… and http://www.climate.gov/news-features/blogs/enso/how-much-do-climate-pat…. Although it was not clear whether the comment implied that these other sources of predictability are somewhat triggered or controlled by ENSO or not, it should be said that some of them may at least partially be so controlled, although they also likely have their own independent component. A point of differentiation between ENSO and these other phenomena is that ENSO tends to be better predicted than the other patterns, and MUCH better predicted once it has locked into one of its two phases (El Nino or La Nina), normally by September or October. (Note that this year is an exception, where even in November it is not entirely clear whether we will have a weak El Nino or not this winter, as the atmosphere has not completely been playing ball even if the SST has recently clearly exceeded the minimum threshold). Applying the idea of multi-faceted controls to analog forecasting, such a forecasting tool should be more effective if it were able to capture several phenomena instead of just ENSO alone. Such analog forecast systems have been developed. The main problem, however, is that the period of record from which to find analog matches is usually only several decades, and looking for more ways to define a good match (not just for ENSO) makes it even harder to find such a match. So the basic flaw in analog forecasting (lack of enough possible past cases to choose from) bites us even more severely when we look for a match in several dimensions instead of just one or two. As for localized, downscaled forecasts, I believe they are possible to the extent that the local data are built into the forecast system. Once the analog year(s) are picked, the resulting forecast can be applied to anything, whether the predictability is good or poor. To summarize my response, I say that analog forecasts may become slightly better (for both large-scale climate anomaly predictions or more downscaled, localized ones) when more dimensions are included in the analog search (e.g., more than just ENSO), but that the increment in value is not large because of the lack of predictability in the non-ENSO phenomena (with the possible exception of long-term climate change-related trends) and particularly because of the lack of a huge sample of past cases.
The model forecast regarding
I love this! Here is my own idea :)
Add new comment